Tweaks and Mathematical Diversions

Pinky Retirement, , ,

Introduction

In the first part of this post I look at tweaking the model through improved formulas. Some of the formula that I used earlier were conservative in the sense that I made approximations which tended to reduce the overall spend. I rectify this in the first part of the post. In the second part I look at some observations on the possibility of modelling using closed equations rather than using optimization routines in Excel. This would be preferable, as it would then be possible to remove optimization routines, which are cumbersome and prone to non-optimal solutions. This post looks at the mathematical side of the blog and can be skipped if you are more interested in financial tools and strategies. The symbols I have used for variables are defined in “End Notes” of the Retirement Calculations post.

Tweaking the Model

Some of the earlier equations are (pretty good!) approximations that can be improved. For example, I have described some of the formulae as “conservative”. This means that I have made an approximation that reduces the overall spend. I look to rectify this here. I also spotted a few errors which I also fix. I anticipate that these changes will not have much effect on the overall result, and will result in an overall slight increase.

Correction to Super return rate

I spotted an error in my excel implementation whereby I used 6.0% when working out the new Super at 60. I should have used 5.5% (the rate for year 59). The formula for the return rate is correct; my implementation wasn’t. If I correct this my annual average spend goes from $87,348.47 to $87,250.11.

Correction to Expenditure deduction when working out next year Cash/Super

When working out the next year’s cash (and next year’s Super when there is no longer any cash), you need to deduct the expenditure for the previous year. The formula for updating the Cash I originally used was this:

{\displaystyle C_{i+1}=C_{i}(1+B_{D})+(D_{i}+I_{i}-E_{i}(1+I_{Y}))(1+\frac{B_{D}}{2})}

Note that the amount I am deducting due to expense during the year is {\displaystyle E_{i}(1+I_{Y})}. Now Ei  was defined as “Expenditure during year i”. Let’s tighten up this definition to “Expenditure during year i in year i dollars”. Then {\displaystyle E_{i+1}=E_{i}(1+I_{Y})} remains correct. But the amount spent during year i is not {\displaystyle E_{i}(1+I_{Y})} as this would imply that prices are inflation adjusted values for the entire year, whereas at the start of the year there is no inflation, for example. And it is not Ei, as this would imply no inflation throughout the year. The correct amount spent is:

{\displaystyle E_{i}\lim_{n \to \infty }\sum_{i=0}^{n-1}e^{\frac{i}{n}I_{C}}=E_{i}\int_{0}^{1}e^{xI_{C}}dx=E_{i}\frac{(e^{I_{C}}-1)}{I_{C}}=E_{i}\frac{I_{Y}}{I_{C}}}

where:

{\displaystyle I_{C}=ln(1+I_{Y})}

and the updated equation for the new value of cash is:

{\displaystyle C_{i+1}=C_{i}(1+B_{D})+(D_{i}+ I_{i}-\frac{E_{i}I_{Y}}{I_{C}})(1+\frac{B_{D}}{2})}

If I make the change, the annual spend changes from $87,250.11 to $88,454.41.

Cash Calculations – Use the correct rate

Banks normally quote their interest rate as the daily rate. That is, if the Interest rate is BD then to work out the value of an asset worth x after n days, you would use this formula:

{\displaystyle New Value = x \ (1+\frac{B_{D}}{365})^{n}}

So that means the annual rate is not 1 + the daily rate. To find the annual rate we need to solve:

{\displaystyle 1+B_{Y}=(1+\frac{B_{D}}{365})^{365}, B_{Y} = Yearly Rate, B_{D} = Daily Rate }

So, for example, for a daily rate of 3.2%, the yearly rate is 3.2516%. If I use the yearly rate rather than the daily rate, the new equation becomes:

{\displaystyle C_{i+1}=C_{i}(1+B_{Y})+(D_{i} +I_{i}-\frac{E_{i}I_{Y}}{I_{C}})(1+\frac{B_{Y}}{2})}

where

{\displaystyle B_{Y}=(1+\frac{B_{D}}{365})^{365}-1}

If I change the Interest rate from the daily rate to the yearly rate when working out the value of cash for the following year, average spend goes from $88,454.41. to $88,486.26 (not too much of a difference!).  

Interest on changing assets

To work out the value of an asset that starts at zero and is increasing (or decreasing) at the same continuous rate, I assumed that the interest earned on the asset is the Interest times half the value of the increase. So, say I earn V dollars over a year with a yearly interest rate of BY , then I assumed that the interest earned is BY ( V  / 2). However, the correct increase in value is given by the equation:

{\displaystyle \lim_{n\rightarrow \infty } \sum_{i=1}^{n}\frac{V}{n} e^{B_{C}(1-\frac{i}{n})} = V\int_{0}^{1}e^{B_{C}(1-x)}dx=\frac{V}{B_{C}}(e^{B_{C}}-1)=V\frac{B_{Y}}{B_{C}}}

Where:

{\displaystyle B_{C}=ln((1+\frac{B_{D}}{365})^{365}-1)}

So, the new formula for Cash is now: For {\displaystyle C_{i}(1+B_{Y})+(D_{i}+ I_{i}-\frac{E_{i}I_{Y}}{I_{C}})\frac{B_{Y}}{B_{C}}} >= 0

{\displaystyle C_{i+1}=C_{i}(1+B_{Y})+(D_{i}+ I_{i}-\frac{E_{i}I_{Y}}{I_{C}})\frac{B_{Y}}{B_{C}}}

For {\displaystyle C_{i}(1+B_{Y})+(D_{i}+ I_{i}-\frac{E_{i}I_{Y}}{I_{C}})\frac{B_{Y}}{B_{C}}} < 0

{\displaystyle C_{i+1}=(C_{i}+D_{i}+I_{i}-\frac{E_{i}I_{Y}}{I_{C}})(1+B_{Y})-(D_{i}+ I_{i}-\frac{E_{i}I_{Y}}{I_{C}})\frac{B_{Y}}{B_{C}}}

So, if I use this rather than the approximation, the average spend rate is now $88,487.72 rather than $88,486.26. i.e. hardly any difference. Because this change significantly complicates the formula and only makes a very minor change, I will keep with the original formula.

Superannuation Deductions

After the cash runs out, to work out the Super value from the previous year, I multiplied the Super at the end of the year by the Super return rate. Given that the Super is decreasing during this period, I am understating the amount of Super I have each year as I am missing out on the interest on the funds that are consumed throughout the year. This is another case of interest being earned on a continuously changing asset. This is the original formula I used for Super:

{\displaystyle S_{i+1}=(1+R_{i})(S_{i}+C_{i}+D_{i}+I_{i}-E_{i}(1+I_{Y}))+\frac{B_{D}C_{i}^{2}}{2E_{i}(1+I_{Y})}+P_{i}H(i=N)}

The first term is for the increase in Super due to Super returns, the second term is due to the interest received on Cash during the one year that Cash does not fully fund expenses, and the last term is the house being sold and incorporated into Super. If I now include the growth in the Super funds that are being consumed during the year and also make the changes already discussed to date, and also assume that Cash will be moved to Super at the start of the year (so that I can remove the second term), then the equation becomes:

{\displaystyle S_{i+1}=(1+R_{i})S_{i}+(C_{i}+D_{i}+I_{i}-\frac{E_{i}I_{Y}}{I_{C}})(1+\frac{R_{i}}{2})+P_{i}H(i=N)}

If I change these formulas, the average spend goes from $88,486.26  to $89,894.52

Correcting the Pension Rates

I made a couple of errors in the Pension rates. I used rates a bit earlier than the September 2014 rates, I didn’t include the full value of the pension (I missed out the energy and pension supplements), and most importantly I used the non-homeowner rate for the asset test full pension threshold rather than the homeowner rate. If I make these corrections, the average spend goes from $89,894.52 to 90,120.49, or an increase of about $226.

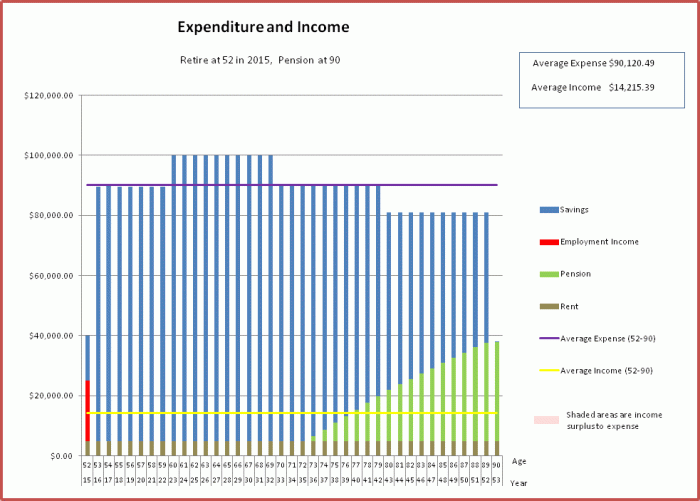
Final Spending Pattern Graph

After all these changes, here is the final spending graph:

image1

Tweaking Conclusions

In conclusion, the approximations in the original formula were not too far off the mark, and, as expected, the changes have resulted in a slight increase in expense per year. The main issues with the original formulas are:

  • I originally worked out the new Super from the old Super by multiplying the Super at the end of the year by the return rate. This results in missing out on interest on funds that are being consumed during the year. Correcting this causes about a $1500 increase in average spend per year.
  • I originally worked out the amount of money spent during year i as the amount earmarked for expenditure (in year i dollars) multiplied by the inflation rate. This is too much, as goods and services at the beginning of the year are not subject to the full inflation figure. If I correct this, it results in an increase in average spend per year of about $1200.

…Mathematical Diversions

Simple Model without the Age Pension, fixed spend per year

Let’s look at trying to is solve equations which model a system where there is no age pension, and where the spend each year is fixed. If f(t) is the function that describes the amount of super at time t, then we have:

{\displaystyle f(t+ \Delta t)=f(t)+\Delta tf(t)R_{C}-\Delta tEe^{I_{C}t}} and {\displaystyle f(0)=S}

This is saying that a small increase in t results in an increase in Super in proportion to the increase in t multiplied by the rate of return on super, multiplied by the value of Super, less the expense rate modified for inflation multiplied by the increase in t. It is also saying that at time 0 (when you retire), the value of Super is S. or:

{\displaystyle {f}'(t)=f(t)R_{C}-Ee^{I_{C}t}}, with {\displaystyle f(0)=S}

This is an ordinary differential equation or ODE. In general ODEs do not have “closed form” solutions. However this one does. Here is the solution:

{\displaystyle f(t)=\frac{Ee^{I_{C}t}}{R_{C}-I_{C}}+Ce^{R_{C}t}}

Using {\displaystyle f(0)=S}, we can solve for C to get:

{\displaystyle f(t)=Se^{R_{C}t}-E(\frac{e^{R_{C}t}-e^{I_{C}t}}{R_{C}-I_{C}})}

Let’s see how this compares this with the model using excel and solver. If I remove the reductions in spending at 70 and 80 in the excel model, then I get a spend of $115,207 (in year 65 dollars) and the value of Super (S) at 65 to be $2,002,208.41 (again in year 65 dollars). If I set f(0) to be this value of Super, and solve for E for which f(25) = 0 (i.e. Super at 90 is zero), then I get E = $115,254, or about 0.04% out. The reason for the difference is most likely the continuous model more accurately reflecting the reality of the interplay between the reduction in Super due to spending and the increase due to returns.

Simple Model without the Age Pension, reduction in spending in later years

Let’s look at the situation where again there is no pension, but this time spending is reduced later on, as described in “Retirement Calculations”. Assume that at time n after retiring we reduce spending by a factor of p. Then we have the following:

{\displaystyle f(t)=\frac{Ee^{I_{C}t}}{R_{C}-I_{C}}+Ce^{R_{C}t} = Se^{R_{C}t}-E(\frac{e^{R_{C}t}-e^{I_{C}t}}{R_{C}-I_{C}})}, for t < n

and

{\displaystyle f(t)=\frac{pEe^{I_{C}t}}{R_{C}-I_{C}}+C_{1}e^{R_{C}t}}, for t>=n

Then as f is continuous, we need

{\displaystyle \lim_{\delta t\rightarrow 0}f(n-\delta t)-f(n+\delta t) = 0}

or

{\displaystyle Se^{R_{C}n}-E(\frac{e^{R_{C}n}-e^{I_{C}n}}{R_{C}-I_{C}})=\frac{pEe^{I_{C}n}}{R_{C}-I_{C}}+C_{1}e^{R_{C}n}}

We also require that f(25) = 0.

If we solve first for C1 in the above equation, and then for E in the equation f(25)=0, we get:

{\displaystyle E=\frac{-S(R_{C}-I_{C})}{pe^{25(I_{C}-R_{C})}-1+(1-p)e^{n(I_{C}-R_{C})}}}

Lets compare this with the Excel model. If we set n = 10, and p = 0.9, then the excel model come up with $118,605. The above equation comes up with $118,654. Again, about 0.04% difference.

We can do similar tricks to get expressions for additional reductions, e.g. reduction by q at time m.

Age Pension with assets test only and Super as the only asset.

I originally thought it wouldn’t be possible to derive equations for the Super when you throw in the Age Pension. However, it is. It’s just that the equations become a nasty and in the end, you need to use numeric methods to derive constants such as expense, the age of getting access to the Pension, the age of getting the full pension. Also, to analyze mathematically, I have assumed that all variables change continuously, which, although a good approximation, doesn’t exactly reflect reality. That is, I assume, for example, that your pension is paid continuously and it is also increased continuously as your assets and income decrease.

I solve this case (age pension with assets test, Super only asset) as an example. Let C1 be the time at which you first get access to the pension and C2 be the age that you get the full pension. Also, in order to simplify, I will use g(t), the real value of Superannuation (and set IC to zero in all equations). Then we have:

{\displaystyle g'(t) = g(t)R_{C}-E }        for  t<C1 and where {\displaystyle g(C_{1}) = P_{UL} }

{\displaystyle g'(t) = g(t)R_{C}-E+ (\frac{P_{UL}-g(t)}{P_{UL}-P_{LL}})P_{FP}}       for C1 < t < C2 and where {\displaystyle g(C_{2}) = P_{LL} }

 and

{\displaystyle g'(t) = g(t)R_{C}-E + P_{FP}}          for  t>C2

Using {\displaystyle g(0)=S}, we get:

{\displaystyle g(t)=Se^{R_{C}t}-\frac{E}{R_{C}}(e^{R_{C}t}-1)}     for t<C1

Using {\displaystyle g(C_{1}^{+})=P_{UL}}   we get

{\displaystyle g(t)=\frac{E(P_{UL}-P_{LL})-P_{UL}P_{FP}}{R_{C}(P_{UL}-P_{LL})-P_{FP}}(1-e^{(t-C_{1})(R_{C}-\frac{P_{FP}}{P_{UL}-P_{LL}})})+P_{UL}e^{(t-C_{1})(R_{C}-\frac{P_{FP}}{P_{UL}-P_{LL}})}}

for C1 < t < C2

and using {\displaystyle g(C_{2}^{+})=P_{LL}} we get

{\displaystyle g(t)=\frac{E-P_{FP}}{R_{C}} +e^{(t-C_{2})R_{C}}(P_{LL}-\frac{E-P_{FP}}{R_{C}})}   for t>C2

We can now use these equations to solve for E, C1 and C2:

{\displaystyle g(a)=0 }. where a is the age at which we are planning to have no Super remaining

{\displaystyle g(C_{1}^{-})=P_{UL}}

{\displaystyle g(C_{2}^{-})=P_{LL}}

Using the above, it is possible to derive an equation which only contains the variable E. This is shown below:

{\displaystyle P_{LL}=\frac{E(P_{UL}-P_{LL})-P_{UL}P_{FP}}{R_{C}(P_{UL}-P_{LL})-P_{FP}}+}

{\displaystyle \frac{P_{UL}R_{C}(P_{UL}-P_{LL})-E(P_{UL}-P_{LL})}{R_{C}(P_{UL}-P_{LL})-P_{FP}}e^{a(R_{C}-\frac{{P_{FP}}}{P_{UL}-P_{LL}})}+}

{\displaystyle(\frac{(P_{LL}R_{C}-E+P_{FP})(SR_{C}-E)}{(P_{FP}-E)(P_{UL}R_{C}-E)})^{(1-\frac{P_{FP}}{R_{C}(P_{UL}-P_{LL})})}}

Note that if we set

{\displaystyle P_{FP}=0}

Then the above equation collapses to:

{\displaystyle e^{aR_{C}}(SR_{C}-E)+E=0}

which is expected as this is the equation if there is no pension.

If we use the excel and set the investment property and rent to zero, eliminate the pension income test, remove the reductions in spending at 70 and 80, set inflation to zero, set the real Super return rate  to 3.26%, then the real value of Super at 65 is $1.36M, and the spend is $93,039.

If we use this value of S in the formula above, and change the interest rate to a continuous rate (3.2%) rather than the yearly rate (3.3%), and use numerical methods (actually Excel goalseek) to solve for E we get a value of $93,996.. This is quite a bit out compared with the other results (about 1.0%). Looking into this in detail, it is easy to see the cause of the discrepancy. The main issue is that in the formula the part pension is increasing throughout the year and so Super is not depleted as fast as in the excel model where the part pension only increases once a year. The excel model reflects reality, as your assets are only updated with Centrelink once a year (for July, entered in August and February).

Mathematical Diversions Conclusions

In conclusion, it is possible to derive equations that model the amount of Super you have, and the level of your expenditure. These equations can remove the need for optimization routines. However any kind of complication, such as the pension, rapidly results in an escalation in the effort required to derive the equations.

  • For the simple case where there is no Age pension and level of spending is the same (in real terms) every year, there is a simple closed form expression for the level of Super and the amount of spend.
  • For a slightly more complicated case where the level of spending is reduced by a fixed factor, there is also a relatively simple closed form expression for amount of Super and spending levels. Iterative equations for subsequent reductions can also be derived.
  • The Age Pension significantly complicates things. It is possible to derive relatively simple equations for the level of Superannuation, but these are in terms of constants which do not have closed form expressions. In order to derive these constants (Expenditure level, age of start of part pension, age of start of full pension), numerical methods are required as the equations relating the constants cannot be used to derive closed form expressions.

For the moment, I recommend remaining with Excel Optimization routines, as this allows model changes with relatively little effort.

Leave a comment